近日，中国科学院软件研究所蔡少伟团队在逻辑约束求解器研究中获得新突破，SAT求解器和SMT求解器研究上的成果被重要期刊和会议录用，并在SAT、MaxSAT和SMT竞赛中斩获佳绩。 

　　求解器被誉为“工业软件之魂”，是继芯片与操作系统之后的国之重器。命题逻辑可满足性问题（SAT）和可满足性模理论问题（SMT）是两个最重要的逻辑约束问题，SAT是命题逻辑上的约束求解问题， SMT是一阶谓词逻辑上的约束求解问题。它们不但在自动定理证明、软件工程等学术研究中有广泛应用，更是信息安全、集成电路设计自动化和软件验证等领域的底层计算引擎。 

　　2022年8月5日，SAT会议正式公布了SAT和MaxSAT的比赛结果。在SAT比赛中，蔡少伟团队以明显优势获得了SAT比赛主赛道并行组冠军和NoLimits 赛道冠军（主要参与者包括蔡少伟研究员及其博士生张昕荻和硕士生陈志翰）。在MaxSAT比赛中，该团队赢得了几乎大满贯的好成绩：在总共6个赛道中获得5个冠军和1个亚军（主要参与者包括蔡少伟研究员及其博士后初一，其中1个冠军是与华为理论实验室的雷震东、东北师范大学的王艺源等人合作获得）。 

　　值得一提的是，蔡少伟团队与国际上SAT研究的另一个主要团队（包括Armin Biere等人）合作的一篇SAT混合求解方法的论文以“Better Decision Heuristics in CDCL through Local Search and Target Phases.”为题，发表在人工智能著名期刊Journal Of Artificial Intelligence Research上。这篇文章为SAT混合求解方向提供了系统性的理论参考。 

　　近两年，该团队开始转向更具挑战的SMT求解方向。SMT求解器的软件架构复杂，开发和维护工程难度大；而且SMT求解器体量庞大，目前的主流求解器，如Z3，CVC5，Yices2等都具有几十万甚至上百万行的代码量；此外，还需要开发者拥有扎实深厚的数学和逻辑学基础。因此SMT求解器的开发技术门槛比较高。 

　　2022年8月11日，在FLoC (Federated Logic Conference，国际联合逻辑大会 )的IJCAR（国际联合自动推理会议）会议上宣布了SMT 2022比赛结果。蔡少伟团队研发的SMT求解器Z3++在比赛中获得线性算术理论和非线性算术理论的多项第一，并在Model Validation的所有赛道综合评分中求解能力领先。其总分获得FLoC奥林匹克竞赛颁发的2块金牌（大赛共设6枚金牌2枚银牌）。这是国内团队首次在FLoC奥林匹克竞赛的SMT比赛中取得金牌。FLoC每四年举办一次，对数理逻辑和计算机科学社区产生重要影响。 

　　Z3++求解器是基于国际主流求解器Z3的衍生求解器，由蔡少伟研究员发起和领导，主要参与者包括他的博士生李博涵、张昕荻、赵梦宇和来自晞德软件公司的林锦坤博士，以及詹博华副研究员和他的硕士生王忠汉。Z3++针对其参与的各个理论都进行了深入的优化。对于位向量理论，Z3++采用了词级别和位级别的重写规则来化简约束；对于整数算术理论，该团队创新性地开发了首个针对整数算术理论的局部搜索求解器；对于非线性实数算术理论，该团队实现了可行域一致性检测并在NLSAT框架下实现了胞腔采样投影。Z3++显著地改进了著名的Z3求解器，其相关创新技术以“Local Search for SMT on Linear Integer Arithmetic”为题发表在理论计算机顶级会议CAV 2022上。 

　　本次夺冠是蔡少伟团队继去年在SMT比赛中首次取得整数差分逻辑冠军后的又一次重大突破。相较于去年因单一理论取得第一，本次夺冠覆盖的理论更为广泛，也更为重要。团队现已将Z3++开源（https://z3-plus-plus.github.io）用于帮助更多研究人员及时学习Z3++相关技术，同时推动更多国内相关方向的研究人员对SMT求解器进行更深入地研究。 

　　蔡少伟团队重视学术研究和工程实践的结合，提出的创新想法最终都能实现为求解器。研究成果多次在国际比赛获奖，并且应用于多个重要的工业场景。该团队还通过举办闭门论坛、专题训练营及新媒体科普等形式，为推动约束求解领域产业生态建设作出积极贡献。 

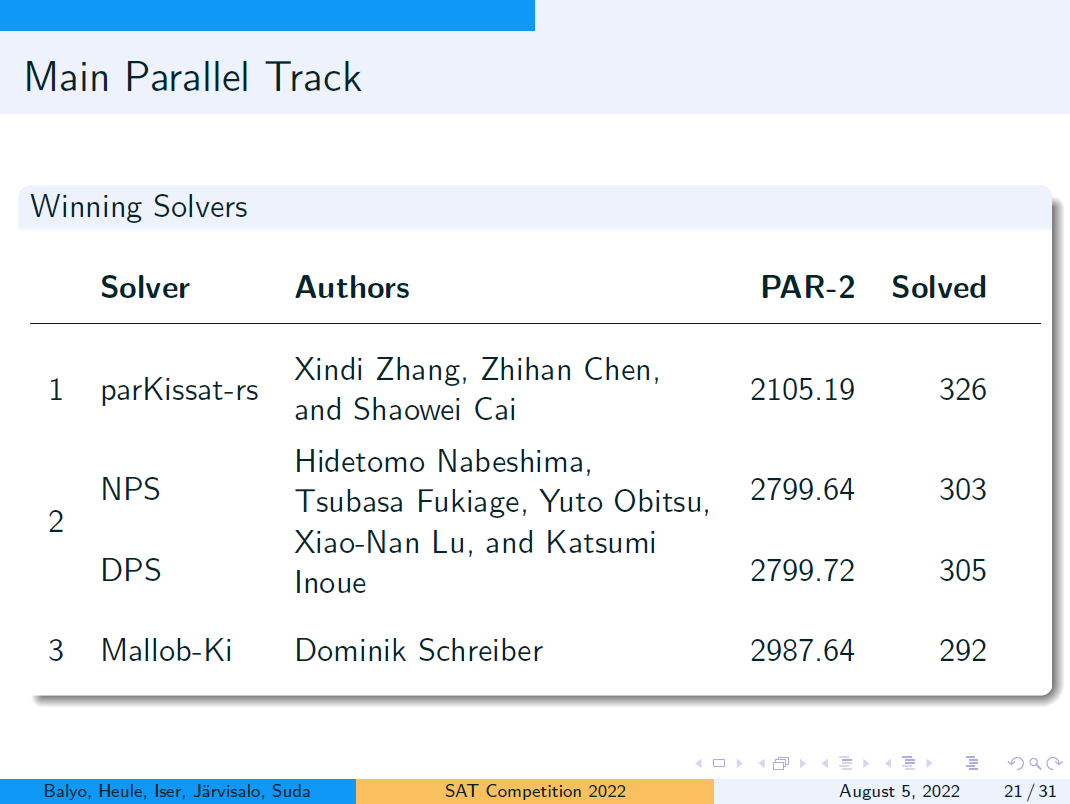
（在SAT比赛中以明显优势获得主赛道并行组冠军）

（在国际联合逻辑大会(FLoC)奥林匹克竞赛SMT比赛中获得2枚金牌）