近日，中国科学院软件研究所基础软件与系统重点实验室（计算机科学国家重点实验室）蔡少伟研究员、量子软件、薛白研究员三个研究团队的论文均作为“Regular Papers”被形式化验证领域国际旗舰会议Computer Aided Verification(CAV 2024)录用，研究成果涉及可满足性模理论分布式求解、量子系统定量模型检测、控制系统高精度可达集下近似的高效计算等方面的工作。量子软件团队还有一篇论文作为“Tool Papers”被CAV 2024条件录用，研究成果涉及量子系统可达性检测工具。

在可满足性模理论分布式求解方面，蔡少伟研究团队论文Distributed SMT Arithmetic Theories Solving Based on Dynamic Variable-level Partitioning（第一作者博士生赵梦宇，通讯作者蔡少伟），首次提出了一个基于变量级别划分方法的动态并行框架，不仅为划分方法提供了新的研究方向，也为其他理论上的变量级划分提供了一定探索空间。

动态并行框架图

可满足性模理论（SMT）是形式化方法与自动推理的一个重要方向，它研究在某些特定理论下（如等式理论和无解释函数、数组理论、位向量、线性和非线性算术）的一阶逻辑公式可满足性的判定方法。在算术理论方面，目前大部分SMT求解器主要基于串行求解，相关工作集中在如何改进串行SMT求解器中的求解技术和启发式方法。面对计算资源与算力日益充足的今天，研究团队尝试采用并行和分布式的方法来充分利用算力，以提高SMT问题的求解性能。

研究团队将提出的方法应用到目前国际最先进的求解器CVC5、OpenSMT2、Z3，与基求解器的求解结果相比，仅是8核的并行求解，平均成功求解实例就增加了3495个，求解速度提高约30%。该方法与前沿并行求解技术相比也有显著提升，并且在非线性理论上表现尤为突出。

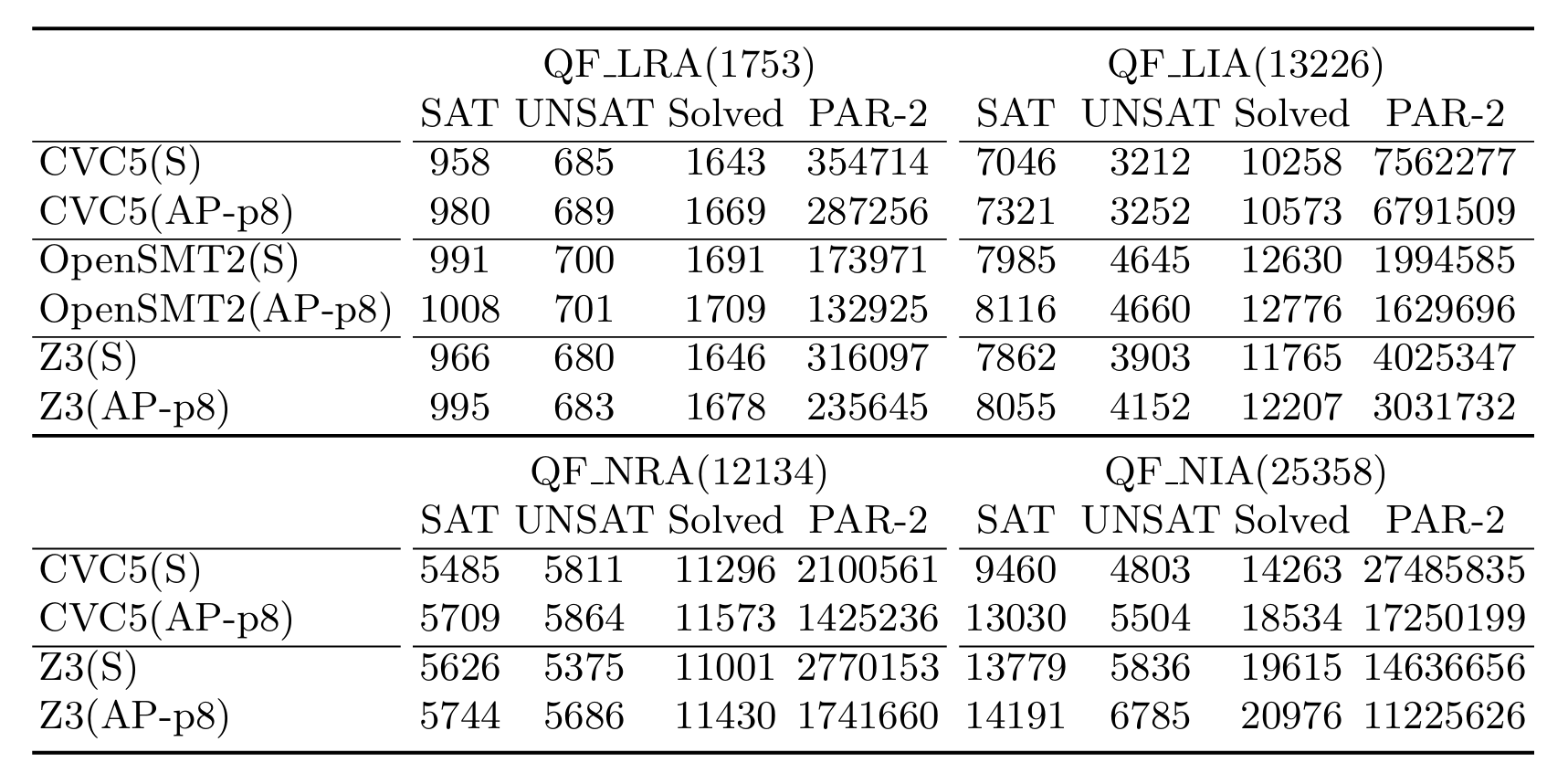
对比基求解器的实验结果

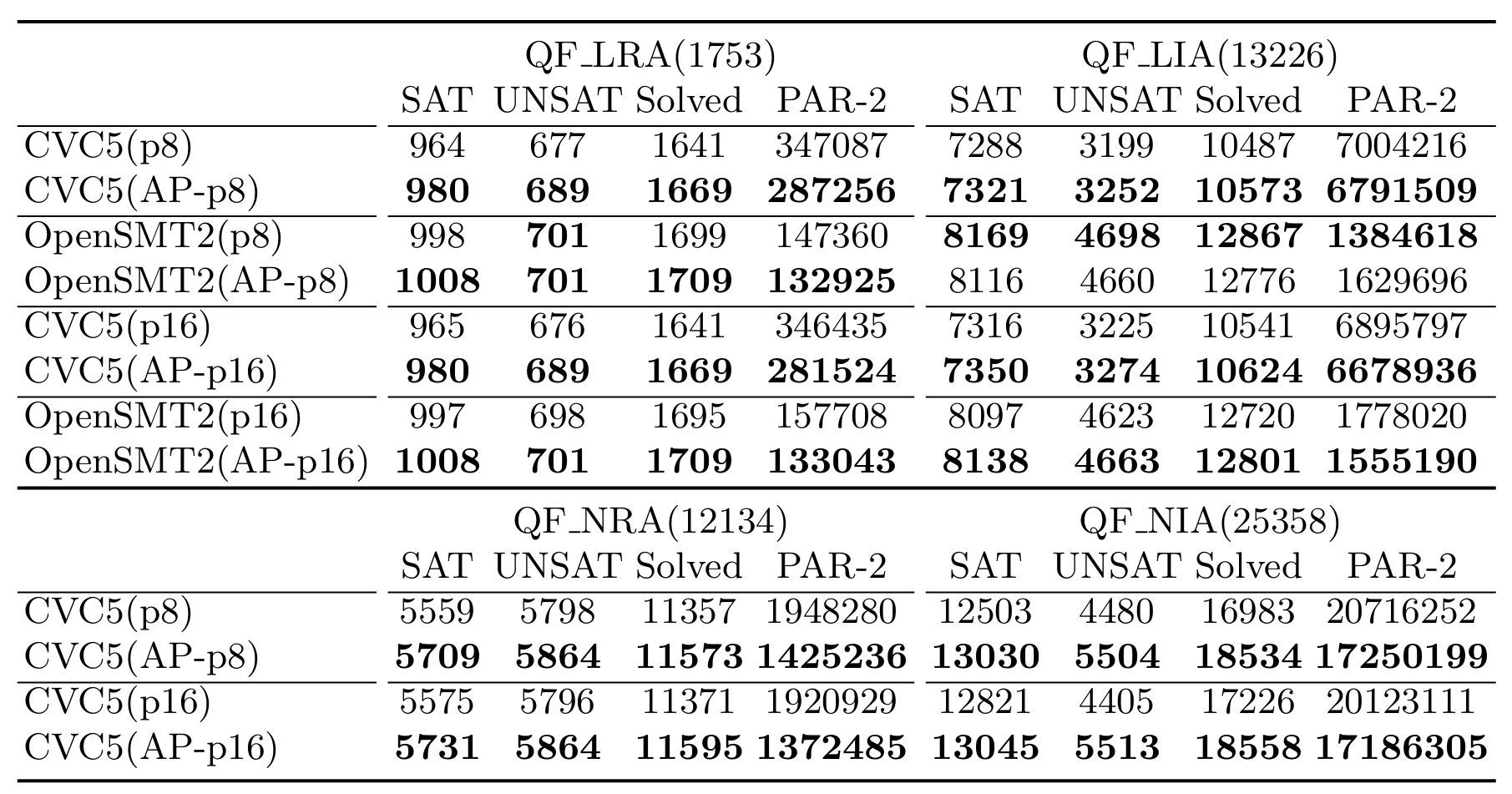
对比前沿并行求解技术的实验结果

工具链接：https://github.com/shaowei-cai-group/AriParti

在量子系统定量模型检测方面，量子软件研究团队的论文Measurement-based Verification of Quantum Markov Chains（第一作者官极副研究员）提出了一种量子线性时序逻辑MLTL（Measurement-based Linear-time Temporal Logic），用来描述量子系统的定量性质。MLTL以经典线性时序逻辑LTL为基础，引入了量子原子命题，可推理量子系统状态被测量后的概率分布的定量时序性质。研究团队还基于量子马尔可夫链模型对MLTL公式进行近似验证，发展了模型检测算法，并成功应用于量子游走时序性质的验证。实验结果不仅证实了量子游走相较于经典随机游走的优势（STOC 2001），更发现了量子游走独有的新现象，为设计高效量子算法提供了理论支持。同时，该工作将模型检测线性时序性质方法的应用从仅适用于经典概率系统拓宽至更广泛的量子系统，对于量子计算机的软件验证具有重要意义。

在控制系统可达集高精度下近似的高效计算方面，薛白研究团队的论文Inner-approximate Reachability Computation via Zonotopic Boundary Analysis（第一作者博士生任德金）针对全对称多胞体初始集合（zonotope），提出了一种高效的边界提取及分割方法，有效提升了可达集下近似（下近似为准确可达集的子集）计算的精度，并基于C++语言开发了可达集计算工具BdryReach。该成果为基于可达性分析的系统错误发现、路径规划、控制器形式设计等应用研究提供了良好基础。

提高可达集计算精度的传统方法需要将初始集合细分为小勒贝格测度的集合，再分别计算每个小集合的可达集，使用此方法计算成本较高，特别是对于高维系统。为解决此问题，薛白研究团队在过去十年间，提出了针对连续系统（如常微分方程、时延微分方程）和神经网络的边界可达性理论方法，用于高效计算高精度可达集上、下近似（上近似为包含准确可达集的集合）。相关论文详见：https://lcs.ios.ac.cn/~xuebai/publication.html。边界可达性理论方法从拓扑角度分析发现无需初始集合内点，仅利用初始集合边界即可计算可达集。由于边界测度远小于整体，因此有助于降低计算成本并提升计算精度。在实际应用中，可以通过细分边界来优化初始集合边界。但现有技术在处理全对称多胞体等特殊集合时，缺乏高效且精确的边界提取和细分方法，影响了可达集高精度下近似的高效计算。

为此，研究团队提出了一种算法，即采用边界矩阵和铺展矩阵，将多胞体边界的处理转化为对矩阵元素的操作来降低时间和空间复杂度，从而有效提取全对称多胞体的边界，并将其划分为互不重叠的子多胞体。团队还利用一种更灵活的可达集近似收缩策略，使得可达集下近似结果更为准确。团队还基于C++语言开发了可达集计算工具BdryReach。实验表明，基于7个从二维到十二维的常微分方程系统，BdryReach在基准场景、更长时间区间以及更大初始集合场景中比已有工具CORA在可达集下近似计算方面具有更高的精度和执行效率。

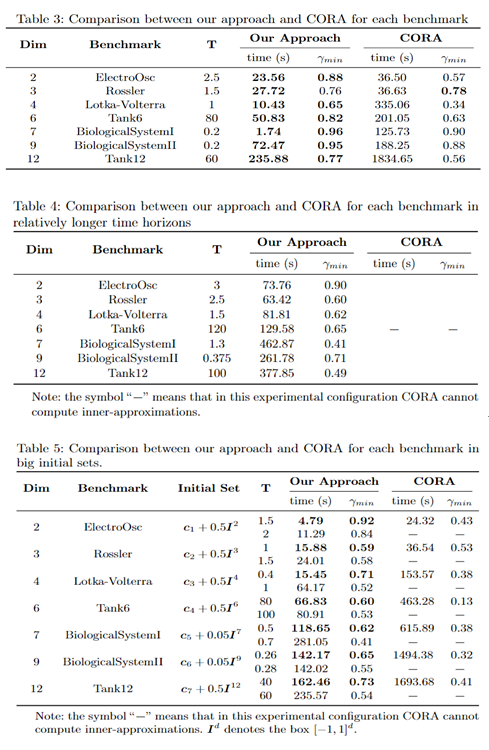
BdryReach与CORA在三种场景下的实验对比

BdryReach工具链接：https://github.com/ASAG-ISCAS/BdryReach

在量子系统可达性检测工具方面，量子软件研究团队的工具论文QReach: A Reachability Analysis Tool for Quantum Markov Chains实现了第一个用于检测量子马尔科夫链系统可达性的工具QReach。QReach工具的创新性主要体现在两方面：一是采用了最新的决策图技术Context-Free Language Ordered Binary Decision Diagram (CFLOBDD)来刻画量子态与量子电路，该技术相比此前的决策图模型具有更紧致的表示能力；二是对之前量子马尔科夫链可达性分析的结论进行了优化，得到了算法复杂度上的提升。

研究团队使用量子随机游走、repeat-until-success等量子电路对QReach工具进行了测试，结果表明该工具能有效提高搜索可达空间的准确性和规模性，可以为对更复杂的量子系统进行模型检测提供支持。